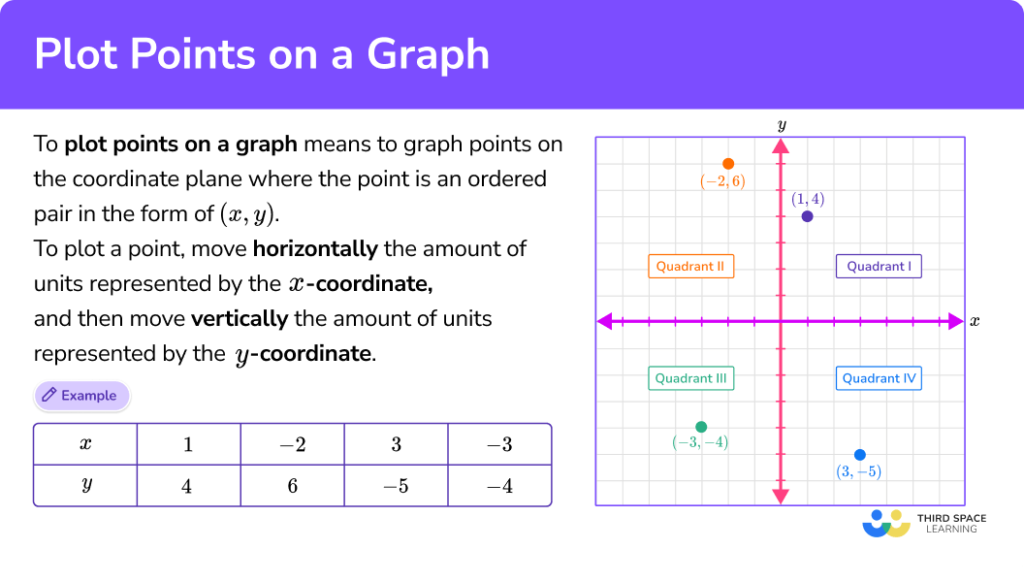
✅ Pour vérifier l’alignement de points, calculez la pente entre chaque paire de points. Si les pentes sont égales, les points sont alignés.
Pour vérifier si plusieurs points sont alignés sur un graphique, vous pouvez utiliser plusieurs méthodes, dont l’analyse visuelle et les calculs de pentes. La méthode la plus courante consiste à s’assurer que la pente entre chaque paire de points est identique. Cela signifie que si vous avez trois points A, B et C, les pentes AB et BC doivent être égales pour que les points soient considérés comme alignés.
Nous allons explorer différentes techniques pour déterminer l’alignement des points sur un graphique. Nous commencerons par des méthodes graphiques, où nous examinerons des représentations visuelles. Ensuite, nous aborderons des méthodes algébriques, en utilisant des équations de droites et des calculs de pentes pour effectuer des vérifications précises. Enfin, nous fournirons des exemples pratiques et des conseils pour vous aider à appliquer ces méthodes efficacement.
Méthodes graphiques
Une des manières les plus simples de vérifier si des points sont alignés est de les tracer sur un graphique. Si les points semblent se trouver sur une même ligne droite, il est probable qu’ils soient alignés. Toutefois, cette méthode peut être subjective et dépendante de votre perception. Pour une analyse plus rigoureuse, vous pourriez vouloir passer à des méthodes numériques.
Méthodes algébriques
Pour déterminer l’alignement de plusieurs points numériquement, vous pouvez utiliser la formule de la pente, qui est donnée par :
Pente (m) = (y2 - y1) / (x2 - x1)
En utilisant cette formule, vous pouvez calculer la pente entre chaque paire de points. Si toutes les pentes calculées sont égales, alors les points sont alignés.
Exemple de calcul de pente
Considérons trois points A(1, 2), B(2, 4) et C(3, 6) :
- Pente entre A et B : mAB = (4 – 2) / (2 – 1) = 2
- Pente entre B et C : mBC = (6 – 4) / (3 – 2) = 2
Étant donné que mAB = mBC, les points A, B et C sont alignés.
Conseils pour la vérification d’alignement
- Utilisez un logiciel de graphique pour faciliter la visualisation des points.
- Vérifiez les coordonnées des points pour éviter les erreurs de saisie.
- Considérez d’utiliser des outils statistiques qui peuvent automatiser ces calculs.
Méthodes de calcul pour déterminer l’alignement des points
Vérifier si plusieurs points sont alignés sur un graphique peut se faire à travers différentes méthodes de calcul. Ci-dessous, nous allons explorer plusieurs techniques qui permettent de déterminer l’alignement de ces points de manière précise et fiable.
1. Utilisation de l’équation de la droite
Une des méthodes les plus courantes consiste à utiliser l’équation de la droite qui passe par deux points. L’équation peut être écrite sous la forme :
y = mx + b
où m est la pente et b est l’ordonnée à l’origine. Pour déterminer si trois ou plusieurs points sont alignés, suivez ces étapes :
- Calculez la pente m entre deux points, par exemple (x1, y1) et (x2, y2) :
- m = (y2 – y1) / (x2 – x1)
- Utilisez cette pente pour déterminer l’ordonnée à l’origine b :
- b = y1 – mx1
- Vérifiez si les coordonnées des autres points satisfont l’équation de la droite.
2. Vérification par les pentes
Une autre méthode consiste à comparer les pentes entre chaque paire de points. Si les pentes sont identiques, alors les points sont alignés. Pour trois points (x1, y1), (x2, y2) et (x3, y3), vous pouvez calculer :
m1 = (y2 – y1) / (x2 – x1
m2 = (y3 – y2) / (x3 – x2)
Si m1 = m2, les points sont alignés. Voici un exemple :
| Points | Pente |
|---|---|
| (1, 2) et (3, 4) | 1 |
| (3, 4) et (5, 6) | 1 |
| (1, 2) et (5, 6) | 1 |
Dans cet exemple, les pentes sont identiques, ce qui montre que les points sont bien alignés.
3. Méthode des déterminants
Une approche plus mathématique consiste à utiliser les déterminants. Pour trois points, si le déterminant de la matrice suivante est égal à zéro, alors les points sont alignés :
| x1 y1 1 |
| x2 y2 1 | = 0
| x3 y3 1 |
Cette méthode est utile pour des ensembles de points plus importants et peut être étendue à plus de trois points en utilisant des déterminants de matrices plus grandes.
4. Utilisation de logiciels de calcul
Enfin, de nombreux logiciels de calcul et de visualisation de données existent pour vérifier l’alignement des points sur un graphique. Des programmes tels que Excel, R ou même Python avec des bibliothèques comme NumPy et Matplotlib peuvent être utilisés pour effectuer ces calculs de manière automatique et visuelle.
Par exemple, voici un code simple en Python qui utilise NumPy pour vérifier l’alignement :
import numpy as np
points = np.array([[1, 2], [3, 4], [5, 6]])
slope = np.diff(points[:, 1]) / np.diff(points[:, 0])
is_aligned = np.all(slope == slope[0])
print("Les points sont alignés :", is_aligned)
En utilisant ces méthodes, vous serez en mesure de déterminer avec précision si plusieurs points sont alignés sur un graphique, en rendant votre analyse de données plus robuste et efficace.
Questions fréquemment posées
Comment savoir si trois points sont alignés ?
Pour vérifier si trois points (A, B, C) sont alignés, vous pouvez calculer la pente entre A et B, puis entre A et C. Si les pentes sont égales, les points sont alignés.
Quelle formule utiliser pour les pentes ?
La formule de la pente entre deux points (x1, y1) et (x2, y2) est (y2 – y1) / (x2 – x1). Appliquez-la pour chaque paire de points pour vérifier l’alignement.
Peut-on utiliser des outils numériques ?
Oui, de nombreux logiciels de graphisme et de calcul, comme Excel ou GeoGebra, permettent de tracer des graphiques et de vérifier facilement l’alignement des points.
Quels sont les signes d’un alignement parfait ?
Un alignement parfait se manifeste par une ligne droite où tous les points sont situés sur la même ligne, sans écart. Cela peut être vérifié visuellement ou par des calculs de pente.
Comment représenter plusieurs points sur un graphique ?
Pour représenter plusieurs points, utilisez un système de coordonnées cartésiennes et tracez chaque point en fonction de ses valeurs x et y. Cela permettra de visualiser l’alignement.
Points clés à retenir
| Points | Conditions d’Alignement |
|---|---|
| 2 Points | Toujours alignés |
| 3 Points | Pentes égales entre chaque paire |
| Plus de 3 Points | Tous doivent respecter la même équation linéaire |
Pour plus d’informations et des conseils, n’hésitez pas à laisser vos commentaires ci-dessous et à consulter d’autres articles sur notre site qui pourraient également vous intéresser !